Epidemia COVID-19 spowodowała znaczące zwiększenie zainteresowania epidemiologią. Od początku pandemii zaczęto tworzyć plany i scenariusze tego, jak dalej kształtować się będą wskaźniki takie jak liczba chorych, zmarłych czy hospitalizowanych. Celem dla którego takie przewidywania się tworzy może być przygotowanie służby zdrowia, informowanie społeczeństwa, zachęcanie do danych działań, ocena potencjalnie podjętych działań i wiele innych. Jednak najważniejszym pytanie to kiedy epidemia dobiegnie końca. Niniejszy artykuł ma za zadanie krótkie przedstawienie, jak dokonuje się opisanych powyżej predykcji i jak tworzy się modele epidemiologiczne.

John Snow kontra cholera na ulicach Londynu

XIX wiek to okres w historii ludzkości, który możemy uznać za początek współczesnej epidemiologii. Głównym celem działania epidemiologów było znalezienie i unieszkodliwienie źródła epidemii. Przykładem może być praca lekarza Johna Snowa, który obserwował kilka epidemii cholery w Londynie. Pierwszą z epidemii jakie widział, w stolicy Wielkiej Brytanii, była epidemia w 1831 roku. Wówczas Snow był jeszcze stażystą, został jednak oddelegowany do leczenia górników. Co istotne zauważył wtedy pewne nieścisłości pomiędzy obserwowanymi faktami, a dominującą ówcześnie teorią miazmatyczną chorób.

Działania podjęte przez Johna Snowa były nieskuteczne ze względu na brak leków, które mogłyby pomóc chorym na cholerę w ówczesnym czasie. Epidemia zakończyła się niespodziewanie w roku 1832, tak samo jak niespodziewanie zaczęła się rok wcześniej. Od roku 1849 Snow badał kolejne przypadki cholery. Jego badania utwierdziły go w przekonaniu, iż jest to choroba przenosząca się z osób chorych na zdrowe, dodatkowo podejrzewał, że przenosi się ona za pośrednictwem wody. Snow przychylał się do teorii zakładającej, iż drobnoustroje patogenne wywołują choroby, pogląd ten był jednak niepopularny. Dlatego by nie zniechęcać innych lekarzy pisał i mówił o truciźnie, by nie wywoływać zbędnego sprzeciwu, ale zmienić podejście innych medyków. Jego działania nie okazały się jednak skuteczne.

Podczas kolejnej epidemii w 1854 roku John Snow zauważył, że ilość osób zmarłych z powodu cholery jest większa w domach, które korzystały z usług dwóch firm wodociągowych pobierających wodę poniżej miejsca spustu ścieków do Tamizy, niż w przypadku trzeciej, która ujęcie wody przeniosła powyżej miejsca zrzutu nieczystości. W roku 1853 niedaleko miejsca zamieszkania Snowa wybuchła epidemia cholery, którą ten skojarzył z zanieczyszczeniem pompy wodnej. Pomimo braku akceptacji dla przypuszczeń Snowa władze lokalne zgodziły się na zablokowanie pompy wodnej, co spowodowało wygaśnięcie epidemii.

Jak mogły wyglądać w rzeczywistości zmagania Johna Snowa? Odpowiedź na to pytanie możesz znaleźć w opowiadaniu Wiktorii Król, pt. Lucy, opublikowanym w tomie Dżuma, kiła i Staphylococcus, czyli epidemie okiem literatów | Aleksander K. Smakosz (red.)

Dalsze starania i nowe informacje jakie John Snow uzyskał w roku następnym potwierdziły, iż źródłem epidemii była skażona pompa wodna na jednej z ulic Londynu. W przypadku przedsiębiorstw wodociągowych, jak i zanieczyszczonej pompy Snow posługiwał się metodami statystycznymi razem z wywiadami by potwierdzić swoje przypuszczenia. Jego praca była na tyle przełomowa, że nie zyskała uznania ówczesnych autorytetów pomimo dużej ilości dowodów i dobrej korelacji przyczyn ze skutkami, jak na dzisiejsze standardy. Jeszcze wówczas dominowała w Europie miazmatyczna teoria chorób. John Snow zmarł w 1858 roku nie dowiedziawszy się o zaobserwowaniu i opisaniu Vibrio cholerae przez Fillipo Pacini, który nie skojarzył tegoż patogenu z cholerą. Współczesne dla Snowa środowisko medyczne i naukowe zapamiętało go jako świetnego anestezjologa, który dopracował metody użycia eteru i chloroformu, dowodem jego świetnych zdolności było dokonanie anestezji na królowej Wiktorii podczas porodu 6. kwietnia 1853 roku.

Pierwszy „model” epidemiologiczny

Za pierwszy „poważny” model epidemiologiczny można uznać trójkąt epidemiologiczny. Jest to koncept, który rozwój epidemii uzależnia od trzech czynników: źródła zakażeń, podatnych osobników i możliwości transmisji lub inaczej nazywając ostatni punkt sprzyjającego środowiska. Źródłem zakażenia mogą być osoby chore, chore zwierzęta w przypadku zoonoz, skażenie środowiska, sprzęt medyczny
i wiele innych – jest to ogólnie rzecz ujmując rezerwuar patogenów.

Podatne osobniki to opis osób, społeczności, zwierząt, stad, roślin, hodowli i innych w zależności od metody opisu i choroby. Możliwość transmisji opisuje wystąpienie warunków umożliwiających przeniesienie patogenu ze źródła na podatne osobniki — może to być stosunek seksualny, kontakt bezpośredni lub pośredni, ekspozycja na aerozol zawierający patogen i wiele innych.

Wykorzystując pojęcie trójkąta epidemiologicznego można zaplanować działania mające za zadanie opanowanie, a nawet zakończenie epidemii. Jako, że zgodnie z założeniami, rozwój epidemii uzależniony jest od występowania wszystkich trzech czynników, to działanie na każdy z nich z osobna lub kilka powoduje zmianę dynamiki epidemii.

Przykładowo możemy wyeliminować z trójkąta osobniki podatne na zakażenie np. poprzez wprowadzenie kwarantanny lub źródło zakażeń izolując osoby chore albo w końcu wpłynąć na możliwość transmisji wprowadzając do użytku środki ochrony osobistej. Zastosowanie trójkąta epidemiologicznego nie pozwala jednak na przewidywanie ilościowe rozwoju epidemii. Nie dowiemy się z jego pomocą ilu nowych zakażeń spodziewać się w danym horyzoncie czasowym, mimo to jest on solidną podstawą do zwalczania epidemii.

Omawiana teoria powstała w XIX wieku; jej założenia mogą wydawać się nam oczywiste, jednak dla wielu wcześniejszych okresów byłaby to teoria przełomowa, która nie uzyskałaby akceptacji. Za ten stan rzeczy odpowiada teoria popularna aż do drugiej połowy XIX wieku — teoria miazmatyczna. Zakładała ona, że choroby przenoszą się za pośrednictwem powietrza określanego jako morowe.

Współczesne modele epidemiologiczne

Współcześnie możemy wymienić kilka kluczowych modeli obliczeniowych stosowanych w epidemiologii, są to:

• model SIS
• model Kermacka-McKendricka (SIR)
• model SEIR
• model sieci społecznych, inaczej nazywany modelem małego świata
  (ang. small world)

Choć wymieniono powyżej kilka standardowych modeli, to należy pamiętać, że są one tylko pewną bazą, rusztowaniem, na którym mogą powstawać nowe, bardziej dopasowane modele. Każdy z nich może zostać rozwinięty, a wraz z tym może wzrastać ich złożoność matematyczna. Różnice te, poza samymi parametrami liczbowymi mogą także obejmować przejścia pomiędzy grupami, co zostanie wytłumaczone w dalszej części artykułu.

Model SIS

Model SIS w skrócie od ang. Susceptible, Infective; Susceptible czyli podatny/wrażliwy, zakażony/zakaźny, podatny opisuje epidemię dzieląc populację na dwie wspomniane grupy: podatnych i zarażonych.

W niniejszym modelu osoba zarażona jest jednocześnie źródłem choroby, który może zarazić osobę z grupy podatnych. Transmisja choroby jest skutkiem kontaktu między osobą z grupy S i I, gdzie każdy kontakt ma pewne prawdopodobieństwo na wystąpienie transmisji. Poza procesem transmisji choroby z osób chorych na zdrowe w modelu uwzględnia się także narodziny zdrowych osobników, które zasilają grupę S oraz śmierć osobników S z przyczyn innych niż choroba, dla której tworzymy model i I z powodu choroby.

Matematyczne ujęcie modelu wprowadza takie pojęcia jak ułamek osób zarażonych i podatnych, liczbę S i I, średnią liczbę interakcji powodujących transmisję, współczynnik rozrodczości i zachorowalności (które w niektórych ujęciach są sobie równe) oraz współczynnik wyzdrowień. Dodatkowym założeniem może być stała liczebność populacji.
Jako oznaczenia poszczególnych wielkości mogą służyć:

N – liczebność całej populacji
nS – liczebność podatnych
nI – liczebność zarażonych
S i I – odpowiednio ułamek podatnych
i zarażonych
S = nS/N i I = nI/N
C – ilość kontaktów pomiędzy osobą
z grupy S, a osobą I; może również być odzwierciedleniem gęstości zaludnienia. Może być proporcjonalna do N lub stała
β – prawdopodobieństwo przejścia S do I w wyniku kontaktu
α – prawdopodobieństwo wyzdrowienia, przejścia I do S

Jako prawdopodobieństwo przejścia możemy uznać wyrażenie CβSI. Jako, że wyrażenie typu Cβ wyraża się często, stosuje się uproszczenie r = Cβ. Zmiany w czasie można zapisać jako:

Jednym z najważniejszych i będących bardzo głośnym medialnie parametrem jest współczynnik reprodukcji R0. Jest to wartość mówiąca nam, czy epidemia przyśpiesza, tj. nowych przypadków zakażeń przybywa R₀ > 1, utrzymuje się na stałym poziomie R₀ = 1, czy wygasa R₀ < 1. Można powiedzieć w uproszczeniu, że wartość R₀ to liczba ile osób zdrowych zarazi średnio jedna osoba chora.

Model Kermacka-McKendricka (Model SIR)

Model Kermacka-McKendricka jest rozwinięciem modelu SIS, dodaje on do dwóch opisanych już klas S i I trzecią R czyli usunięci/nie podatni od ang. Removed. Do grupy R zalicza się osoby, które nabyły odporność lub zostały oddzielone od całej populacji np. poprzez izolację, pobyt w szpitalu, albo zmarły.

W modelu SIR osoba podatna może stać się zarażoną, a zarażona usuniętą. W przeciwieństwie do modelu SIS nie mamy tu do czynienia z przechodzeniem osobników z grupy I do S. Powyższe zdanie można podsumować: kierunek przejść między grupami jest jednokierunkowy i nie jest odwracalny.

W zależności od przyjętych założeń możemy pozwolić wyłącznie na przejścia S do I do R — tak jak wynikało by to ze scenariusza zdrowy, chory, odporny lub zmarły albo pozwolić na przejście S bezpośrednio do R np. w wyniku szczepienia. Dzięki wykorzystaniu modeli możliwe jest nie tylko odpowiednie przygotowanie się do epidemii ale także wprowadzenie aspektów farmakoekonomiki w te przygotowania np. wyliczając jaki procent populacji powinien zostać zaszczepiony, by zahamować epidemię.

Model SEIR

Model SEIR można opisać jako kolejne rozwinięcie modelu SIS. Po dodaniu do modelu SIS grupy R zostaje dodana kolejna grupa oznaczana E od ang. Exposed — wystawiony na działanie (patogenu). Wprowadzenie grupy E daje nam możliwość ujęcia w modelu sytuacji gdy osoba, która uległa zarażeniu sama jeszcze nie zaraża innych, a dopiero po minięciu pewnego czasu, okresu inkubacji, przechodzi do grupy I. Może to być także odzwierciedlenie sytuacji w której nie każda ekspozycja na patogen kończy się aktywną chorobą, tak jak np. w przypadku gruźlicy. Nie każda osoba z grupy E musi stać się I, można wyobrazić sobie sytuację, w której przechodzi ona do grupy R, np. w konsekwencji śmierci niezwiązanej z epidemią.

Opisywany model został użyty do predykcji rozwoju epidemii COVID-19 w Indiach. Dzięki zastosowaniu takiego modelu możemy ocenić konieczność przygotowania służby zdrowia, oraz oszacować konieczną wielkość rezerw leków i sprzętu.⁠ Po pewnych modyfikacjach model ten może uwzględniać również kwarantannę i hospitalizację, co sprawia że jest on bardziej dokładny w przewidywaniu epidemii COVID-19.

Użycie sztucznej inteligencji i baz danych może dać dość dokładne wyniki w przewidywaniu przebiegu oraz szacowaniu pików, tak jak udało się to ocenić chińskim badaczom

Sieci społeczne, model małego świata

Model sieci społecznej, nazywany także modelem małego świata (ang. small world) jest dość złożonym podejściem do opisu epidemii. Jest to bardzo często symulacja komputerowa, w której brane są pod uwagę jednostki i ich kontakty z innymi jednostkami. Symulacja taka ma za zadanie odzwierciedlić złożoną sieć interakcji społecznych, a także przypadkowe spotkania między osobni-kami. Graficzne przedstawienie takiego modelu przypomina drzewa utworzone z kropek reprezentujących poszczególne jednostki, które połączone są między sobą liniami przedstawiającymi interakcję lub transmisję choroby

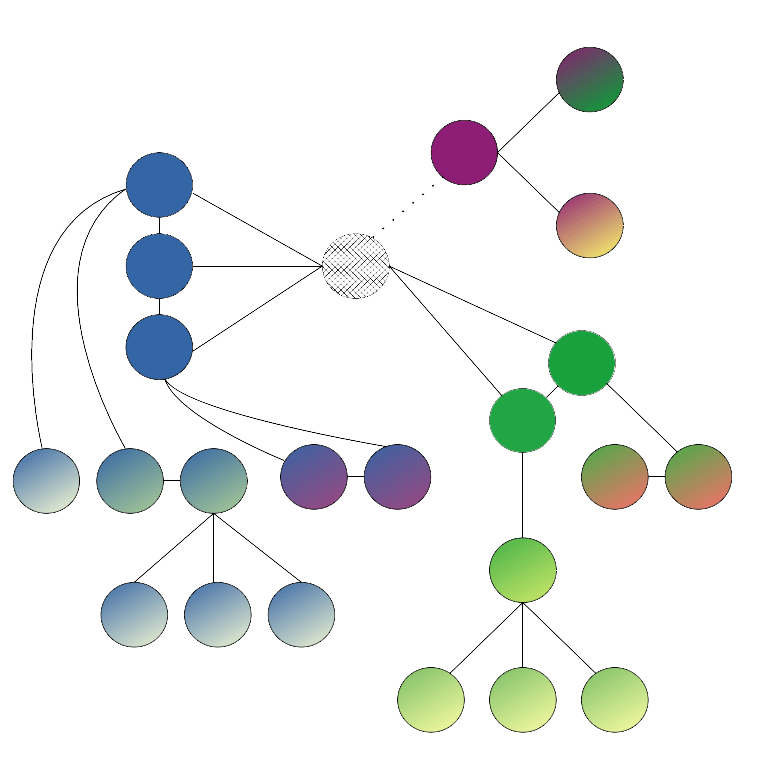
Podsumowanie

Istnieje wiele możliwości przewidywania rozwoju epidemii, które pozwalają nam ocenić jakie środki powinniśmy zabezpieczyć by im zapobiegać, ile osób zaszczepić by wyeliminować daną chorobę, a także kiedy epidemia dobiegnie końca i jakie działania się do tego przyczyniają oraz na ile są skuteczne. Patrząc z perspektywy historycznej epidemiologia przeszła dużą przemianę od odkryć Johna Snowa przez odrzucenie teorii miazmatycznej aż po dzisiejsze możliwości modelowania, a co za tym idzie skuteczniejszego zapobiegania i zwalczania epidemii. Smutnym jedynie wydać się może, że w obecnych czasach, przy dostępności tak wielu środków zapobiegawczych jak szczepionki rośnie niechęć do nich i nieufność w stosunku do nauki.

Bibliografia

• Bartkiewicz, A. (2020). Koronawirus. Czechy: Współczynnik R0 powyżej 1. Epidemia się rozwija – Koronawirus SARS-CoV-2 – rp.pl. https://www.rp.pl/Koronawirus-SARS-CoV-2/201219586-Koronawirus-Czechy-Wspolczynnik-R0-powyzej-1-Epidemia-sie-rozwija.html
• Casanova, J.-L., & Abel, L. (2013). The Genetic Theory of Infectious Diseases: A Brief History and Selected Illustrations. Annual Review of Genomics and Human Genetics, 14(1), 215–243.
• Halliday, S. (2001). Death and miasma in Victorian London: An obstinate belief. British Medical Journal Vol. 323, Issue 7327, 1469–1471.
• Harding, N., Spinney, R. E., & Prokopenko, M. (2020). Population mobility induced phase separation in SIS epidemic and social dynamics. Scientific Reports, 10(1), 1–11.
• Jarynowski, A., & Belik, V. (2018). Choroby przenoszone drogą płciową w dobie internetu i e-zdrowia: kalkulatory ryzyka. Biblioteka Jagiellońska, 101–111.
• Jarynowski, A., & Grabowski, A. (2015). Modelowanie epidemiologiczne dedykowane polsce. Centrum Zastosowań Matematyki.
• Kostyńska, M. (2020). Współczynnik reprodukcji wirusa – co to takiego? https://www.medonet.pl/koronawirus-pytania-i-odpowiedzi/sars-cov-2,wspolczynnik-reprodukcji-wirusa—co-to-takiego-,artykul,27862431.html
• Mostowy, R. (2020). Pandemia koronawirusa: co dalej? | Nauka w Polsce. https://naukawpolsce.pap.pl/aktualnosci/news%2C81241%2Cpandemia-koronawirusa-co-dalej.html
• Nakamura, G. M., & Martinez, A. S. (2019). Hamiltonian dynamics of the SIS epidemic model with stochastic fluctuations. Scientific Reports, 9(1), 1–9.
• Pandey, G., Chaudhary, P., Gupta, R., & Pal, S. (2020). SEIR and Regression Model based COVID-19 outbreak predictions in India. ArXiv Preprint, 2004.00958.
• Rudko, M. Z. (2019). Gry komputerowe jako przykład środowiska dla symulacji epidemii. Rodzaje symulacji w epidemiologii. W: M. Dąsal (red.), Acta Uroboroi – w kręgu epidemii II (s. 137–152). SKN Uroboros.
• Vachon, D. (2005a). Father of Modern Epidemiology. Old News 16(8). https://www.ph.ucla.edu/epi/snow/fatherofepidemiology.html
• Vachon, D. (2005). Doctor John Snow Blames Water Pollution for Cholera Epidemic. Old News 16(8).
• Yang, et al. (2020). Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. Jurnal of Thoracic Disease, 12(3), 165–174.
• Yuexi, S. H., & Sun, P. K. (2020). SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dynamics, 101(3), 1667–1680.
• Zesławska, A. (2013). Modele epidemiologiczne. https://www.impan.pl/~slawek/sem/modele_epidemiologiczne.pdf

Autor

mgr. farm Michał Rudko — magister farmacji (Uniwersytet Medyczny im. Piastów Śląskich we Wrocławiu), obecnie doktorant na Katedrze i Zakładzie Chemii Fizycznej i Biofizyki (UMW). Zainteresowany między innymi chemią w szczególności chemią organiczną, syntetyczną, polimerów, krystalografią, modelowaniem molekularnym i epidemiologicznym oraz historią.

Uwaga

Pierwotnie powyższy tekst został opublikowany w czasopiśmie Pharmacopola, numer 1/2021